学習の精確さを決めているパラメータはどのようなものでしょうか。
ニューラルネットワークには多くのパラメータが絡み合っています。それらを最適に決められるかどうかが、学習の精確性を決定するのです。
パラメータにはざっと以下のようなものが存在します。
- 入力に対する重み付け
- 損失関数
- 活性化関数
学習の精度を高めるには、損失関数を利用します。損失関数とは、正解値と予測値の「差」のようなもので、これを小さくしていくことによって、ニューラルネットワークの精度を上げていくのです。
代表的な損失関数には、二乗和誤差や交差エントロピーなどがあります。
あるノードに向かってくる入力値は、すべて平等に扱われるわけではありません。ある入力値は大きく扱われ、また別の入力値は小さく扱われます。
それぞれの入力値に対して「重要さ」とも言うべきものを定める必要があり、それを重み付けと呼んでいます。
この重み付けが最適かどうかが、損失関数によって計られます。損失関数が最小になるポイントが、学習において目指すべき所であり、その為に重み付けを調整していく過程、それが「学習」なのです。
ニューラルネットワークでは、学習の過程で使用されるデータ量は膨大です。それら一つ一つにおいて現れるすべての損失関数の出力値の和が最小になるように調整していくことになります。
損失関数を最小にするには、損失関数の出力値を重み付けパラメータで微分し(重みが変わると損失関数の出力値が変化する)、重みがどれだけ変われば損失関数がどのように変化するかを見ます。
そして学習のたびに毎回毎回、損失関数が小さくなる方向に、重み付けパラメータを少しずつ動かしていきます。
活性化関数は、ノードに入力された値をどのような規則で「活性」と見なすかを決定付けるものです。次に挙げるものが代表的です。
ステップ関数
シグモイド関数
ReLU関数
ソフトマックス関数
恒等関数
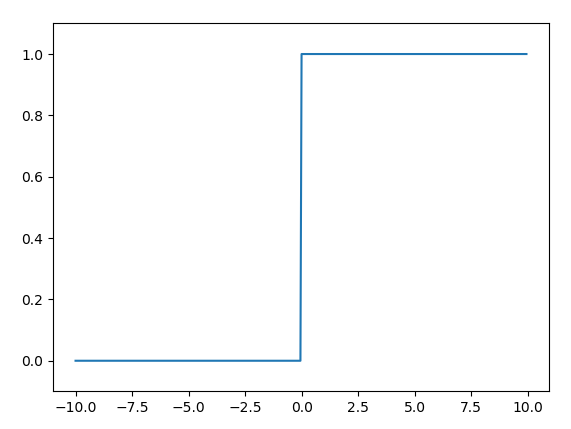
ステップ関数
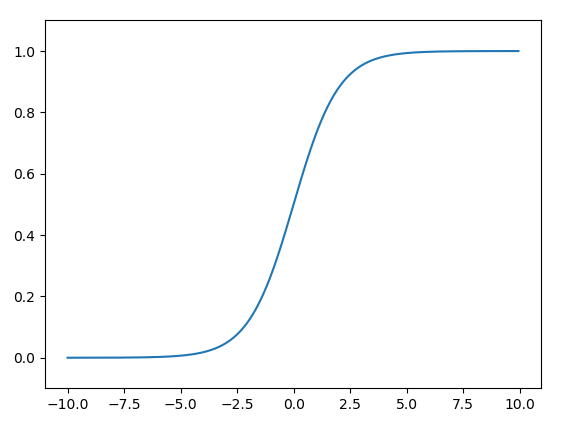
シグモイド関数
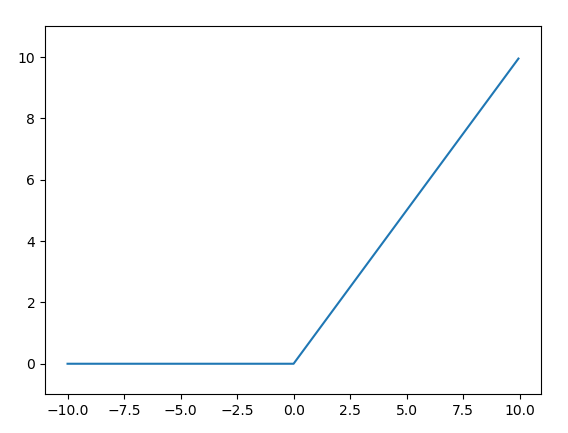
ReLU関数
ニューラルネットワークが扱う典型的な問題は、分類問題と回帰問題に分けられます。
分類問題とは、文字認識や、画像からそれが何であるかを当てるなど、データが何に分類されるか、を判断する問題です。
回帰問題とは、株価の予測など、入力データから何らかの数値を予測するような問題を指します。
出力層に置かれる活性化関数は、そのネットワークが取り扱う問題によって最適なものが異なると言われます。分類問題ではシグモイド関数やソフトマックス関数が、回帰問題では恒等関数が適しているとされています。